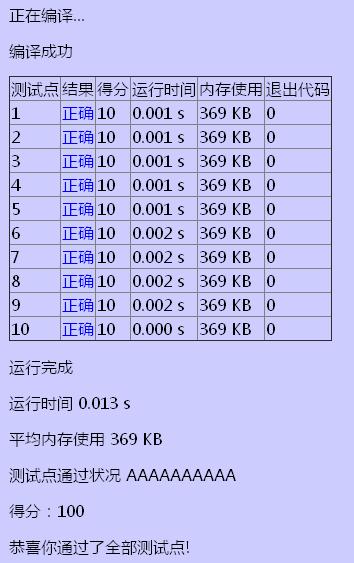
【问题描述】
有 N 个不同的正整数数 x 1 , x 2 , ... x N 排成一排,我们可以从左边或右边去掉连续的 i 个数(只能从两边删除数), 1<=i<=n ,剩下 N-i 个数,再把剩下的数按以上操作处理,直到所有的数都被删除为止。
每次操作都有一个操作价值,比如现在要删除从 i 位置到 k 位置上的所有的数。操作价值为 |x i – x k |*(k-i+1) ,如果只去掉一个数,操作价值为这个数的值。
任务
如何操作可以得到最大值,求操作的最大价值。
Input Data
输入文件 remove.in 的第一行为一个正整数 N ,第二行有 N 个用空格隔开的 N 个不同的正整数。
Output Data
输出文件 remove.out 包含一个正整数,为操作的最大值
约束和提示
3<=N<=100
N 个操作数为 1..1000 之间的整数。
样例
remove.in
6
54 29 196 21 133 118
remove.out
768
说明:经过 3 次操作可以得到最大值,第一次去掉前面 3 个数 54 、 29 、 196 ,操作价值为 426 。第二次操作是在剩下的三个数( 21 133 118 )中去掉最后一个数 118 ,操作价值为 118 。第三次操作去掉剩下的 2 个数 21 和 133 ,操作价值为 224 。操作总价值为 426+118+224=768 。题解: 本题为今天的考试题中最水的一道,哎,鄙人较水,没有写出来,(水呀!水呀!水呀水!),还是来好好总结一下思路吧!!! 首先这是一道动态规划,跟NOIP2007矩阵取数游戏略像,哎,先写一下动态转移方程:i表示从前面取i个,j表示从后面取j个,q[i][j]=max(q[k][j]+w[k+1][i],q[i][k]+w[n-j+1][n-k]),这题败在初始化了,伤不起呀,一定要把q[i][0]和q[0][j]的情况初始化了!! 原程:C++语言:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#define max(a,b) ((a)>=(b)?(a):(b))
using namespace std;
int n,a[110],q[110][110],w[110][110];
int main()
{
freopen ("remove.in","r",stdin);
freopen ("remove.out","w",stdout);
scanf("%d",&n);
for (int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
w[i][i]=a[i];
}
for (int i=1;i<=n;i++)
{
for (int j=i+1;j<=n;j++)
{
w[i][j]=abs((double)(a[j]-a[i]))*(j-i+1);
}
}
for (int i=1;i<=n;i++)
q[i][0]=w[1][i];
for (int i=1;i<=n;i++)
q[0][i]=w[n-i+1][n];
for (int i=1;i<=n;i++)
{
for (int j=1;j<=n;j++)
{
if (i+j>n)
{
continue;
}
int temp1=0;
for (int k=0;k<=i;k++)
{
if (q[k][j]+w[k+1][i]>temp1)
{
temp1=q[k][j]+w[k+1][i];
}
}
int temp2=0;
for (int k=0;k<=j;k++)
{
temp2=max(temp2,q[i][k]+w[n-j+1][n-k]);
}
q[i][j]=max(temp1,temp2);
}
}
int answer=0;
for (int i=1;i<=n;i++)
{
if (q[i][n-i]>answer)
{
answer=q[i][n-i];
}
}
cout<<answer;
return 0;
}
|